W tej lekcji:
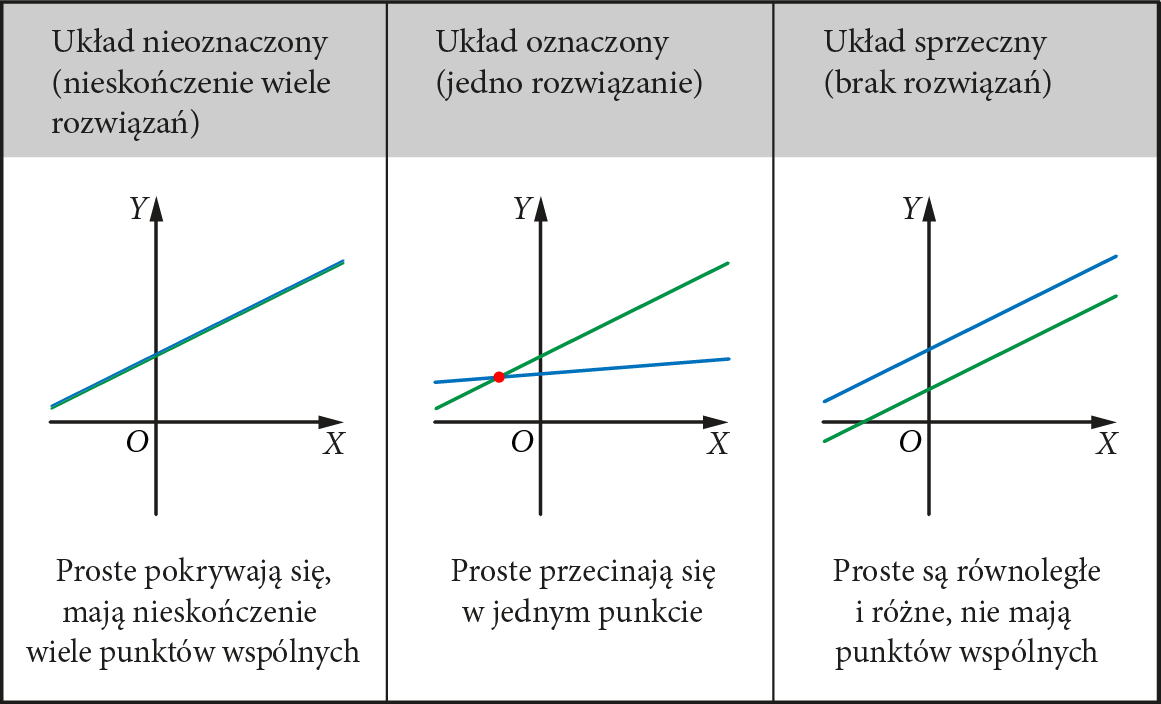
rozwiązywanie układów równań
- Dostęp do 9 przedmiotów
- Płatność co miesiąc
- Zrezygnuj kiedy chcesz!
Nie lubisz kupować kota w worku?
Sprawdź, jak wyglądają lekcje na Dla Ucznia
metoda przeciwnych współczynników
Metoda przeciwnych współczynników rozwiązywania układów równań polega na:
- zauważeniu przeciwnych współczynników przy tej samej niewiadomej lub przekształceniu równań układu w równania równoważne tak, aby otrzymać przeciwne współczynniki,
- dodaniu stronami obu równań i wyznaczeniu jednej niewiadomej,
- utworzeniu nowego układu z równaniem z wyznaczoną niewiadomą oraz drugim dopisanym równaniem (dowolnym: górnym lub dolnym),
- podstawieniu otrzymanej liczby do drugiego równania i jego rozwiązaniu,
- podaniu pary liczb spełniającej układ równań.
wzory skróconego mnożenia
Wzory skróconego mnożenia związane z drugimi potęgami
- Kwadrat sumy
(a + b)2 = a2 + 2ab + b2 - Kwadrat różnicy
(a − b)2 = a2 − 2ab + b2 - Różnica kwadratów
(a + b)(a − b) = a2 − b2
metoda podstawiania
Metoda podstawiania rozwiązywania układów równań z niewiadomymi x i y polega na wyznaczeniu z jednego równania niewiadomej np. y i podstawieniu jej do drugiego równania. Wówczas to drugie równanie staje się równaniem z jedną niewiadomą x, którą wyznacza się za pomocą znanych metod. Aby wyznaczyć niewiadomą y, podstawia się otrzymaną wartość niewiadomej x do równania, które opisuje y. Pary liczb (x, y) są rozwiązaniem układu równań.
rozwiązania równania kwadratowego
Rozwiązania równania kwadratowego ax2 + bx + c = 0 to:
x1 = −b − √Δ2a, x2 = −b + √Δ2a, gdy Δ > 0,
x0 = −b2a, gdy Δ = 0,
gdzie Δ = b2 − 4ac.
Równanie kwadratowe nie ma rozwiązań, gdy Δ < 0.
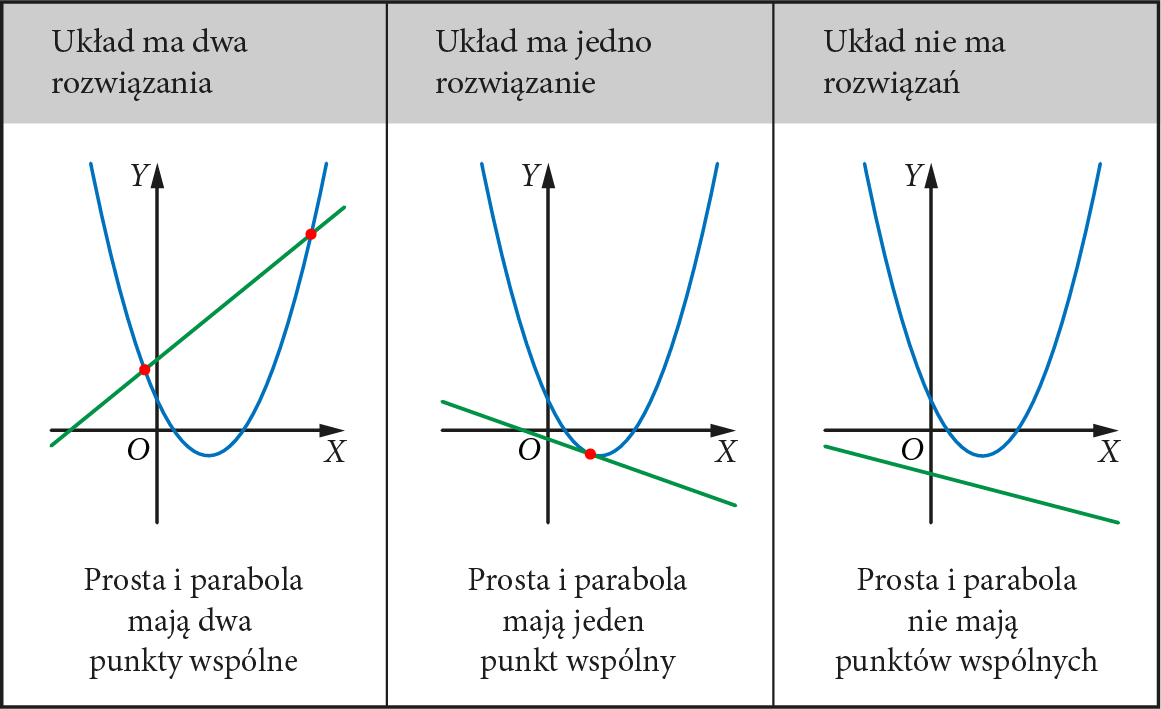
sieczna paraboli
Sieczna paraboli to prosta przecinająca parabolę w dwóch punktach.
styczna do paraboli
Styczna do paraboli to prosta, która z parabolą ma jeden punkt wspólny.