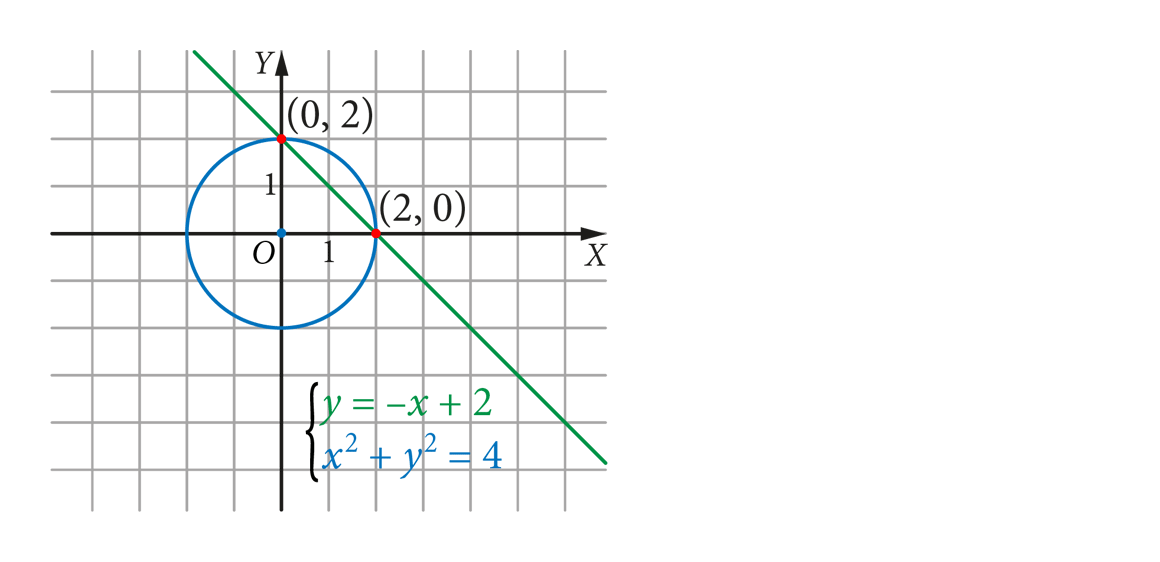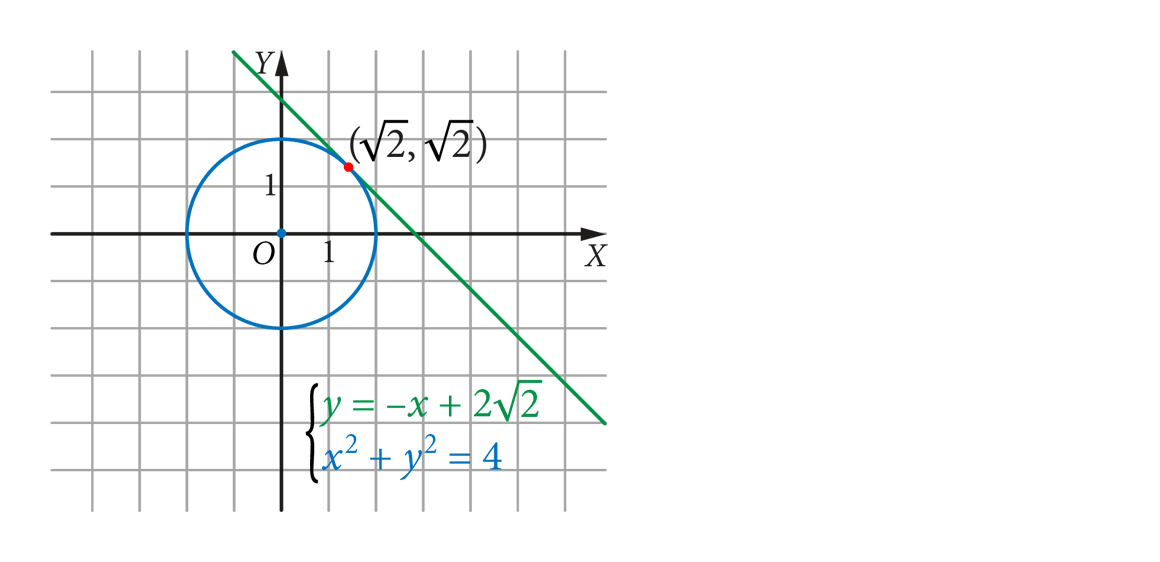Punkty wspólne prostej i okręgu o środku w punkcie (0, 0)
Prosta y = ax + b i okrąg x2 + y2 = r2 są interpretacją geometryczną układu równań
{y = ax + bx2 + y2 = r2
Współrzędne ich punktów wspólnych są rozwiązaniem układu równań.
- Jeśli prosta i okrąg mają 2 punkty wspólne, to układ równań ma 2 rozwiązania.
- Jeśli prosta i okrąg mają 1 punkt wspólny, to układ równań ma 1 rozwiązanie.
- Jeśli prosta i okrąg nie mają punktów wspólnych, to układ równań nie ma rozwiązań.
W tej lekcji:
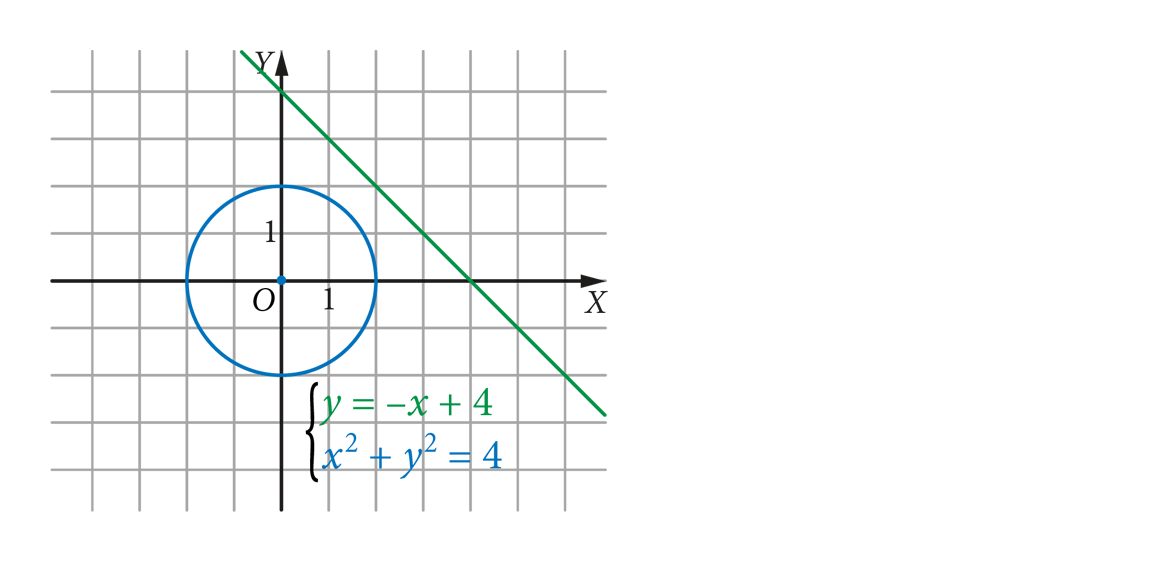
punkty wspólne prostej i okręgu
układy równań z równaniem kwadratowym
- Dostęp do 9 przedmiotów
- Płatność co miesiąc
- Zrezygnuj kiedy chcesz!
Nie lubisz kupować kota w worku?
Sprawdź, jak wyglądają lekcje na Dla Ucznia
Dla Ucznia nauka zdalna liceum nauka zdalna portal
metoda podstawiania
Metoda podstawiania rozwiązywania układów równań z niewiadomymi x i y polega na wyznaczeniu z jednego równania niewiadomej np. y i podstawieniu jej do drugiego równania. Wówczas to drugie równanie staje się równaniem z jedną niewiadomą x, którą wyznacza się za pomocą znanych metod. Aby wyznaczyć niewiadomą y, podstawia się otrzymaną wartość niewiadomej x do równania, które opisuje y. Pary liczb (x, y) są rozwiązaniem układu równań.
rozwiązania równania kwadratowego
Rozwiązania równania kwadratowego ax2 + bx + c = 0 to:
x1 = −b − √Δ2a, x2 = −b + √Δ2a, gdy Δ > 0,
x0 = −b2a, gdy Δ = 0,
gdzie Δ = b2 − 4ac.
Równanie kwadratowe nie ma rozwiązań, gdy Δ < 0.
długość odcinka (odległość między punktami) w układzie współrzędnych
Długość odcinka o końcach w punktach A(xA, yA) i B(xB, yB) jest równa:
∣AB∣ = √(xB − xA)2 + (yB − yA)2
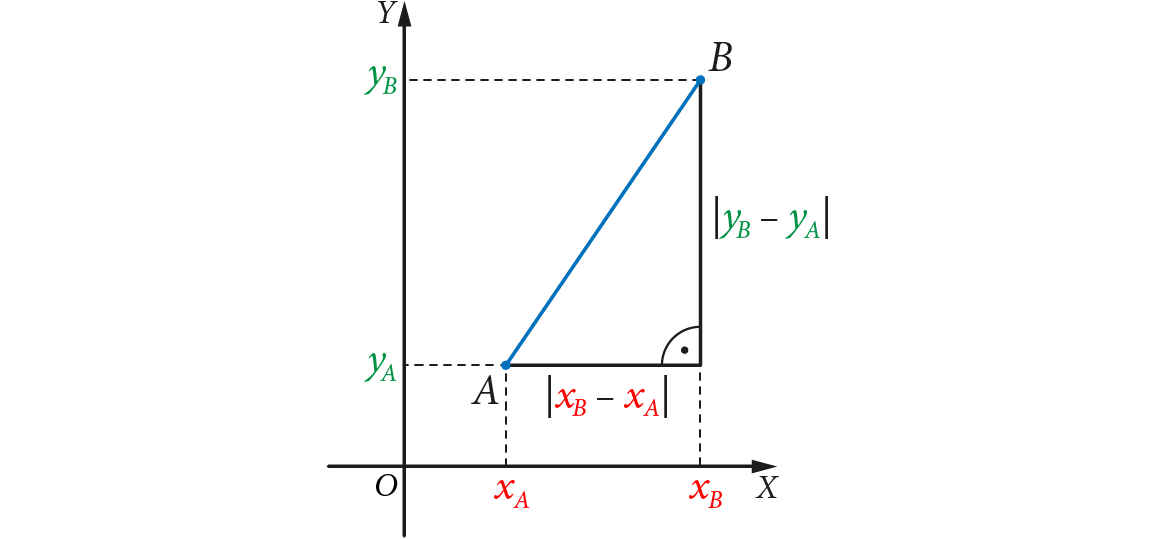
Długość odcinka AB jest również odległością między punktami A i B.
proste prostopadłe
Są to proste, które przecinają się pod kątem prostym. Iloczyn współczynników kierunkowych w równaniach tych prostych jest równy −1.
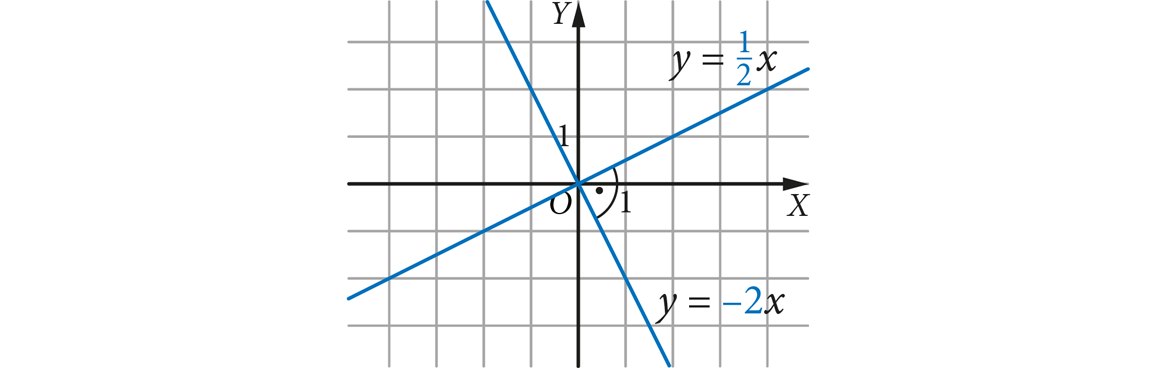
Prostymi prostopadłymi są proste o równaniach np.:
y = −2x i y = 12x, ponieważ 2 ⋅ (−12) = −1
y = −x i y = x + 2, ponieważ −1 ⋅ 1 = −1
y = 23x + 4 i y = −32x + 7, ponieważ 23 ⋅ (−32) = −1