dziedzina
Dziedzina funkcji (zbiór argumentów) to zbiór wszystkich liczb, dla których zostały określone wartości.
zbiór wartości
Zbiór wartości funkcji to zbiór tych liczb, które są wartościami dla argumentów funkcji.
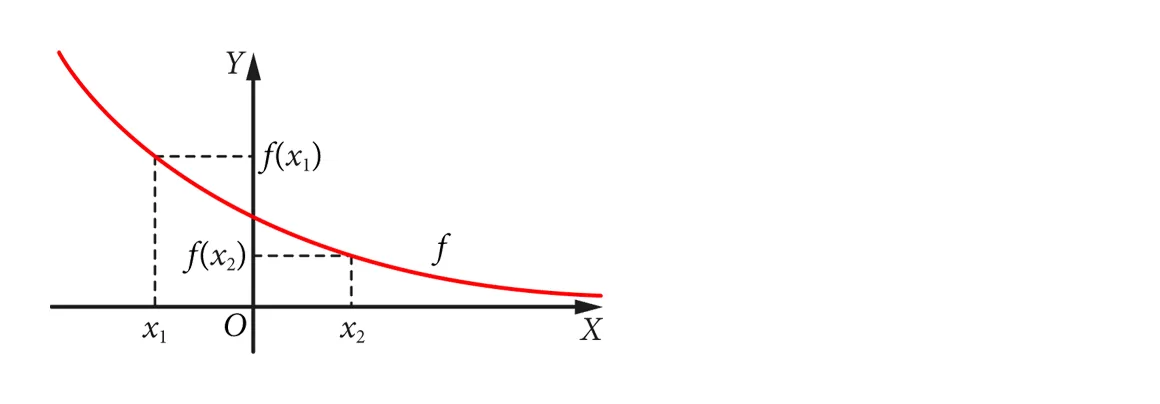
funkcja jest malejąca
Funkcję nazywamy malejącą, jeśli dla dowolnych argumentów x1, x2, spełniony jest warunek:
jeśli x1 < x2, to f(x1) > f(x2)
funkcja jest rosnąca
Funkcję nazywamy rosnącą, jeśli dla dowolnych argumentów x1, x2 spełniony jest warunek:
jeśli x1 < x2, to f(x1) < f(x2)
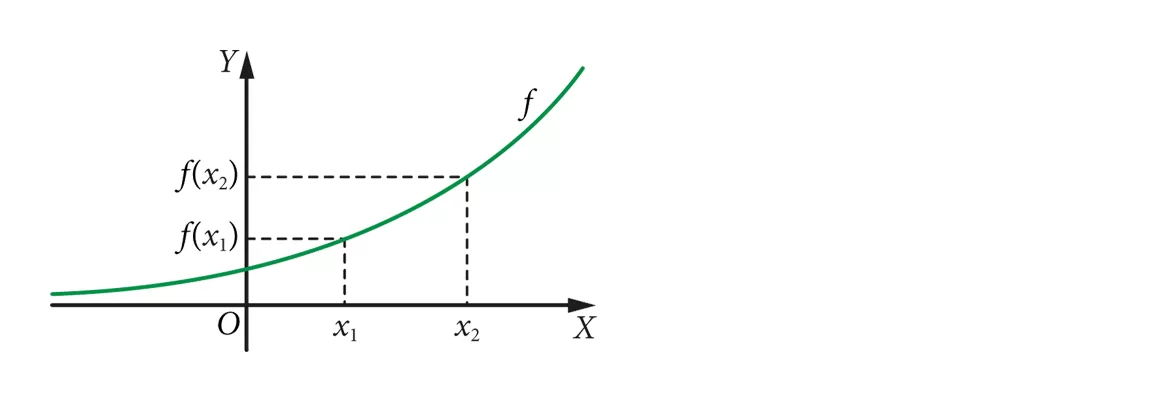
monotoniczność funkcji
Aby opisać monotoniczność funkcji, należy określić, czy jest ona: rosnąca, malejąca, stała, nierosnąca (malejąca lub stała) lub niemalejąca (rosnąca lub stała).
Funkcja może być niemonotoniczna w całej swojej dziedzinie.
Funkcja może być monotoniczna przedziałami.
f(x) > 0
Aby wyznaczyć argumenty, dla których funkcja przyjmuje wartości dodatnie, można rozwiązać nierówność f(x) > 0 lub odczytać te argumenty z wykresu funkcji (będą to argumenty, dla których wykres funkcji znajduje się powyżej osi OX).
f(x) < 0
Aby wyznaczyć argumenty, dla których funkcja przyjmuje wartości ujemne, można rozwiązać nierówność f(x) < 0 lub odczytać te argumenty z wykresu funkcji (będą to argumenty, dla których wykres funkcji znajduje się poniżej osi OX).
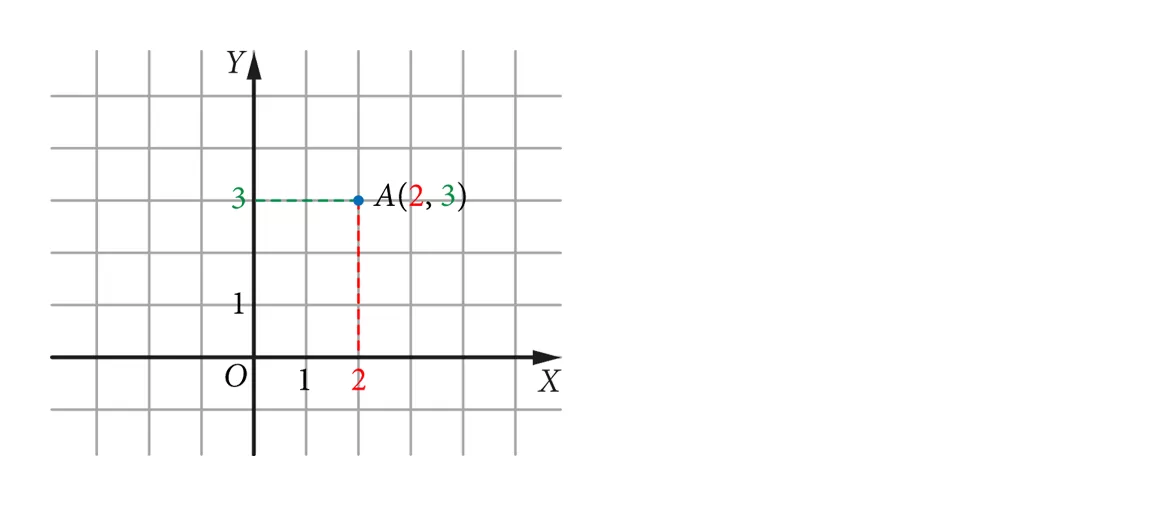
punkt o współrzędnych
Pierwsza współrzędna punktu to liczba na osi OX, druga – to liczba na osi OY.
jak narysować wykres funkcji
Aby narysować wykres funkcji, należy:
- ustalić kształt wykresu
- wyznaczyć kilka punktów należących do wykresu
- zaznaczyć punkty w układzie współrzędnych i poprowadzić przez nie krzywą